Задачка на построение. Вопросы и задачи 80, Геометрия, 10-11 класс, Атанасян Л.С.

Мы давно уже чертили,сохранилось вот

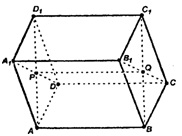
а) Сечение плоскостью АВС₁.
Пл. ВВ₁С₁С || пл. AA₁D₁D по свойству параллелепипеда, отсюда
ВС1 || AA₁D₁D.
Тогда А - общая для плоскостей АВС₁ и AA₁D₁D - плоскости пересекаются по прямой, проходящей через т. А  и параллельной ВС₁ (п. 11,1°).
Плоскости граней АА₁В₁В и DD₁C₁C пересечены плоскостью ABC₁D₁  значит, их линии пересечения параллельны, АВ || C₁D₁.
Вывод: плоскость пересекает грань AA₁D₁D по прямой AD₁; AD₁ ||  ВС₁. Искомое сечение ABC₁D параллелограмм по определению.
б) Сечение плоскостью DCB₁ .
Точка D - общая для плоскостей DCB₁ и AA₁D₁D - плоскости пересекаются по прямой, проходящей через т. D и параллельной прямой СВ₁ (п. 11, 1°). В пл. грани AA₁D₁D проводим такую прямую. Это бу­дет DA₁ (4-угольник DCB₁A₁  - параллелограмм, поэтому DA₁  || СВ₁ ).
Искомое сечение DCB₁A₁ .
в) PQ - отрезок, по которому пересекаются построенные сечения 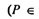плоскостям сечений и Q 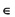плоскостям сечений, PQ - линия  пересечения плоскостей), где Р и Q - центры граней AA₁D₁D и ВВ₁С₁С.