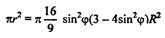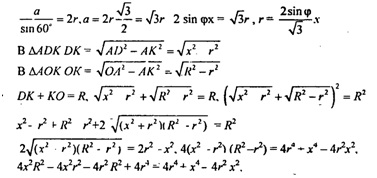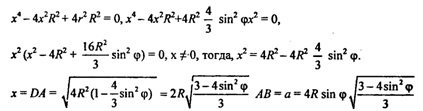Точки А, В, С и D лежат на сфере радиуса R, причем... ГДЗ, дополнительная задача 626, Геометрия, 10-11 класс, Атанасян Л.С.

а) Построим DK ┴ плоскости AВС, проведем отрезки КВ, КС. (Чтобы не загромождать рисунок, показан только КA).

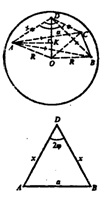
∆DKA - ∆DKB = ∆DKC (по катету и гипотенузе). Следовательно, КА = КВ = КС = r, r — радиус окружности, описанной около ΔАВС Построим отрезок ОТ ┴ плоскости АВС и отрезки ТА, ТВ, ТС
∆ОТА = ∆ОТВ - ΔОТС (они прямоугольные, ОТ — общий катет, OA= ОВ = ОС = R, R — радиус сферы), тогда, ТА = ТВ = ТС = r. r — радиус окружности, описанной около ААВС Выше доказано, что КА= КВ = КС = r. Значит, точки Т и К совпадают и отрезок OD ┴ плоскости АВС
∆ADC - ∆BDC = ∆AОВ (по двум сторонам и углу между ними), следовательно, АВ = СВ — АС, ∆АВС — равносторонний

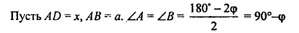
Согласно теоремы синусов

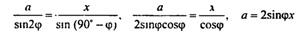
Пусть КA = КВ = КС = r. По теореме синусов для ∆AВС.


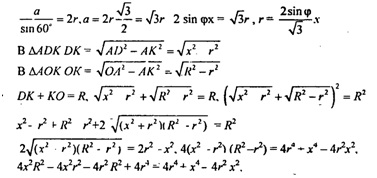
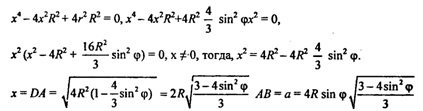
б) Сечение сферы плоскостью ∆ABС является окружность с радиусом

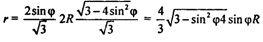
Вычислим площадь сечения: