Сколько центров симметрии имеет... Вопросы и задачи 276, Геометрия, 10-11 класс, Атанасян Л.С.

Она длинная, к сожалению, как-то так...
По определению точка называ­ ется центром симметрии фигуры, если каждая точка фигуры сим­ метрична относительно нее неко­ торой точке той же фигуры.

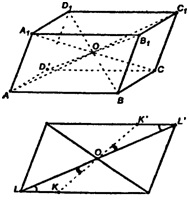
а) Диагонали параллелограмма делятся точкой пересечения пополам. Сечение параллелепипеда  про­извольной плоскостью,  содержа­щей точку О , есть параллело­грамм, стороны которого - линии пересечения секущей плоскости с гранями параллелепипеда. Пусть точки К и К’ произвольные точки противоположных  граней, через которые проходит секущая плоскость. Т.к. ΔLOK- ΔL’OK’ (по стороне и двум прилежащим к ней углам), то ОК =  ОК', а это означает симметрию точек К и К’ относительно точки О.
Поскольку плоскость сечения выбрана произвольно, то любые две точки противоположных граней будут симметричны относи­тельно т. О.
Т.к. диагонали параллелепипеда пересека­ются в одной точке, то точка О - единствен­ная. Отсюда следует, что параллелепипед имеет одну точку симметрии.

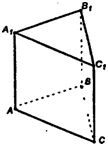
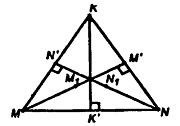
б)   Не имеет центра симметрии. Рассмотрим самый простой случай: построим плоскость, перпендикулярную к боковому ребру призмы и проходящую через середину этого ребра. Она будет плоскостью симметрии правильной призмы.
Возьмем на ребрах точки N и N' симметричны относительно точки N₁. М и М' симмет­ричны  относительно точки М_1. Даже в простейшем случае эти точки не совпа­дают.
в) Двугранный угол не имеет центра симметрии.
г) Середина отрезка - его единст­венный центр симметрии.