Рассмотрите §7 №31 ГДЗ Геометрия 7-9 класс Погорелов А.В.

На прямолинейном шоссе требуется указать место автобусной остановки так, чтобы сумма расстояний от нее до населенных пунктов А и В была наименьшей. Рассмотрите два случая: 1) населенные пункты расположены по разные стороны от шоссе; 2) населенные пункты расположены по одну сторону от шоссе.

1 ответ

ответы

Вадим Ермишен

Пожаловаться

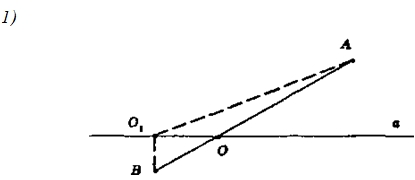
Обозначим шоссе а.
Если А и В лежат по разные стороны от а, то остановка О должна быть в точке пересечения отрезка АВ с а. Если О1 не лежит на АВ, то по неравенству треугольника в Δ АО1В сумма двух сторон треугольника больше третьей стороны; то есть ВО1 + АО1 > АВ, ВО1 + АО1 > ВО + АО, значит, ВО + АО = АВ — наименьшая сумма расстояний от остановки О до населенных пунктов А и В. И точка О — искомая.

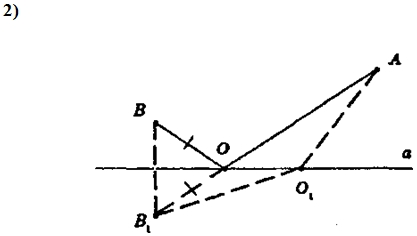
Обозначим шоссе а.
Если А и В лежат по разные стороны от а, то остановка О должна быть в точке пересечения отрезка АВ с а. Если О1 не лежит на АВ, то по неравенству треугольника в Δ АО1В сумма двух сторон треугольника больше третьей стороны; то есть ВО1 + АО1 > АВ, ВО1 + АО1 > ВО + АО, значит, ВО + АО = АВ — наименьшая сумма расстояний от остановки О до населенных пунктов А и В. И точка О — искомая.