Помогите §7 №43 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Даны две окружности с радиусами R1, R2 и расстоянием между центрами d. Докажите, что если каждое из чисел R1, R2 и d меньше суммы двух других сторон, то окружности пересекаются в двух точках.

1 ответ

ответы

Вадим Ермишен

Пожаловаться

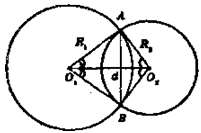
Так как d<R1 + R2R1<d + R2
R2 < d + R1, то можно построить треугольник со сторонами, длина которых R1, R2, d. Обозначим этот треугольник O1O2А, где O1O2 = d, O1A = R1; O2А = R2. По одну сторону от прямой O1O2 расположен Δ O1AO2. Следовательно, по другую сторону от O1O2 можно отложить угол O1O2B, равный углу O1O2A, и угол O2O1B, равный углу O2O1A. Получится ΔO1O2В=ΔO1O2А по стороне и двум прилежащим к ней углам. Значит, O1В = O1A = R1 и O2В = О2А = R2. Значит, точки А и В принадлежат обеим окружностям, а так как две окружности не могут иметь более двух общих точек, то окружности пересекаются в двух и только двух построенных нами точках А и В.
Что и требовалось доказать.