Перпендикулярны ли векторы? ГДЗ, дополнительные задачи 508, Геометрия, 10-11 класс, Атанасян Л.С.

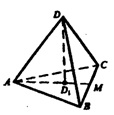
По определению проекции прямая DD₁ перпендикулярна плоскости АВС, т.е. она перпендикулярна всем прямым, лежащим в этой   плоскости.

a) D₁D┴D₁B.
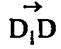— направляющий вектор прямой D₁D;
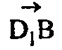— направляющий вектор прямой D₁B. Следовательно, D₁B ┴ D₁D;
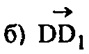также направляющий вектор прямой D₁D, DD₁ ┴ (АВС), т.е. DD₁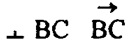— направляющий вектор прямой ВС. Тогда 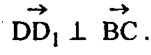Т.к D₁D=-DD₁, то угол φ₁ между DD₁ и плоскостью АВС равен: φ₁=180°-φ, где φ=90° — угол между D₁D и плоскостью АВС;
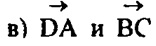— направляющие векторы прямых DA и ВС.
Если 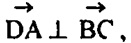то DA -L ВС.
Т.к. тетраэдр ABCD — правильный, то его вершина D проектируется  в центр ∆АВС Если провести в ∆АВС высоту AM, то высота тетраэдра DD₁ пересечется с высотой ААВС в точке D₁, тогда
1 ) СВ ┴ AM, т.к. AM — высота ∆АВС;
2) СВ ┴ DD₁, DD₁ ┴ (АВС);
3^ AM и DD₁ ϵ (DD1A), прямые AM и DD₁ пересекаются.
Из 1), 2) и 3) следует, что СВ перпендикулярна  плоскости DD₁C, значит,  СВ ┴ DA, BC┴.DA.
г) DC и D₁B не перпендикулярны, т.к. прямые DC и D₁B не перпендикулярны. Если бы CD ┴ D₁B, то по теореме, обратной к т. о трех перпендикулярах, CD₁ ┴ D₁B. Но это прямые, содержащие медианы правильного треугольника. Они не перпендикулярны.