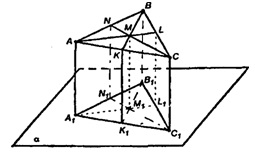
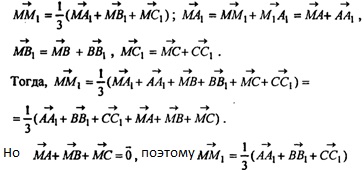Из отрезков AA1, BB1, СС1 выберем наименьший и через эту вершину ΔАВС проведем плоскость, параллельную а. Проведем ме диану AL в ΔАВС и рассмотрим проекцию AL на построенную плос кость.
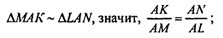
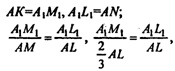 значит
значит 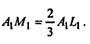
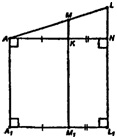
Аналогично проведем медиану CN в ΔАВС и точно так же спроектируем ее на плоскость, параллельную пл. α, из подобия треугольников имеем: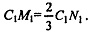
Построим медиану ВК в ΔАВС, тогда 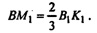
Значит, в ΔА1В1С1 точка М1 есть точка пересечения медиан этого треугольника.
Если М - произвольная точка пространства, а точка М1 - точка пересечения медиан ΔА1В1С1, то имеет место равенство
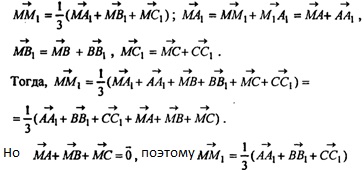
Т.к. 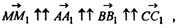 то можно записать равенство на длины векторов:
то можно записать равенство на длины векторов: 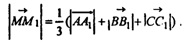
Замечание. Докажем, что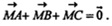
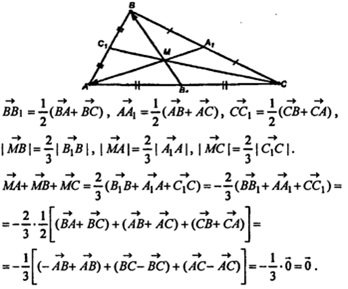
Итак: доказано, что 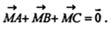
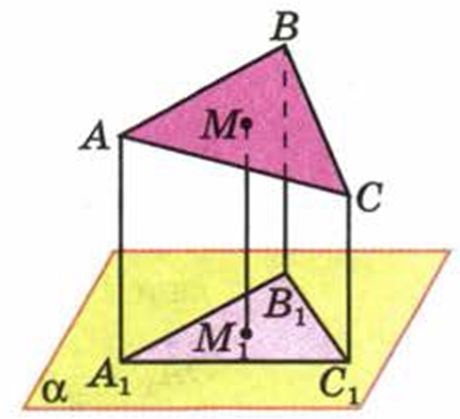
Предположим, что ΔАВС так пересекается с плоскостью а, что точка пересечения медиан лежит в плоскости α. Следовательно ММ1=0, а сумма длин перпендикуляров, проведенных из вершин ΔАВС к плоскости а, конечно же, не равна 0.
Тогда, в случае, когда некоторые стороны ΔАВС пересекаются с плоскостью а, данное равенство может терять смысл.
Ответ: в общем случае - нет.









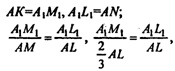 значит
значит