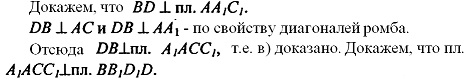Основанием наклонного параллелепипеда является ромб... Дополнительные задачи 295, Геометрия, 10-11 класс, Атанасян Л.С.

СС₁||АА₁   ABCD - ромб. Отсюда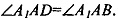

Построим 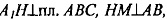 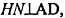отрезки A₁M и A₁N.
Нам   надо   доказать,   что  высота параллелепипеда А₁Н проектирует­ся в точке Н на диагональ АС.
Т.к. по построению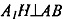 и 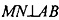то по теореме о 3-х перпендикулярах имеем: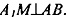
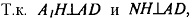то по теореме о 3-х перпендикулярах имеем: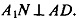
ΔA₁AM=ΔA₁AN, (А₁А - общая, они прямоугольные и имеют по равному острому углу). Отсюда следует, что AM=AN.
ΔAHM=ΔAHN, (т.к. они прямоугольные, гипотенуза АН - общая,
AN=AM).
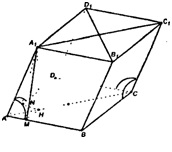
Отсюда следует, что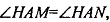то есть точка Н лежит на биссектрисе угла ромба, которая является диагональю ромба; а диа­гонали ромба взаимно перпендикулярны.
Т.к.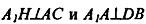(по теореме о 3-х перпендикулярах), но
т.к. А₁А || C₁C, то С₁С || DB.
Утверждение а) доказано.
Докажем, что BB₁D₁D - прямоугольник.
Т.к. D₁B₁  || DB и D₁D || B₁B, то DD₁B₁B - параллелограмм.
B₁B || А₁А, но т.к. доказано, что 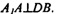Значит, в параллелограмме D₁DВ₁B 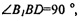и потому данный параллелограмм - прямоугольник.
Утверждение б) доказано.

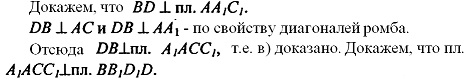
Т.к. пл. BB₁D₁D проходит через прямую 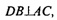то плоскости перпендикулярны.
Мы доказали и пункт г).