Определите вид сечения, проходящего через эти точки. Дополнительные задачи 300, Геометрия, 10-11 класс, Атанасян Л.С.
Давай свой респект)
Построим сечение плоскостью, проходящей через точки Е, F и P.
Построим среднюю линию в ΔABC, EF||AC,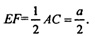
EF || АС, а АС 
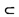пл. DCА, значит,
EF || пл. DCA. Плоскость сечения пе ресечет грань DCA по прямой РК.
Т.к. плоскость сечения проходит через прямую EF, параллельную
плоскости DCA и пересекает плоскость DCA, то линия пересечения
РК параллельна прямой EF.
Построим в грани BDA отрезок FP, а в грани BDC - отрезок ЕК. 4-угольник EFOK и есть искомое сечение. EF || АС, РК || EF || АС,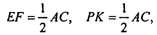 
значит,
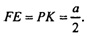Т.к. EF || РК и EF=PK, то EFPK - параллелограмм. Таким образом, ЕК || ЕР, ЕК - средняя линия ΔBCD,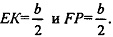 
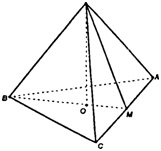
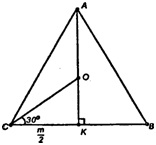
Угол между скрещивающимися прямыми DB и СА равен 90.
Докажем это.
Построим высоту пирамиды DO. Точка О - центр правильного ΔАВС. Продолжим отрезок ВО до пересечения со стороной АС в точке М. В правильном ΔАВС ВМ — высота, медиана и биссектриса, следовательно,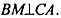
Имеем, что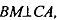
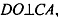тогда по признаку перпендикулярности прямой и плоскости, 
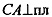BDM, тогда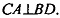 
Значит, т.к.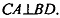 
а РК || СА и ЕК || BD, то 
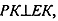и 4-угольник EFPK есть прямоугольник.
SEFPK=PK∙EK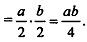 
Ответ: 
