Популярные темы

ЕГЭ

3273 ответа

Русский язык, Химия, Геометрия, Обществознание, Физика

Школа

9 класс, 8 класс, 11 класс, 10 класс, 7 класс, 6 класс, 4 класс, 5 класс, 1 класс, 2 класс

Учебники

Разумовская М.М., Габриелян О.С., Рудзитис Г.Е., Цыбулько И.П., Атанасян Л.С., Цветков Л. А.

Психология

Отношения, Любовь, Красота, Воспитание

Показать все

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания "Останкино"?

Часто ищут

36 вариантов ответов ЕГЭ по русскому языку 2017. И. П. Цыбулько Средний балл по предметам за ЕГЭ в 2017 году?Лабораторная 1. Физика 7 класс №10. вопросы к §1-3. Составьте в тетради таблицу. Рудзитис, Фельдман 8 класс химия Спишите отрывки из басен И. А. Крылова, верно употребляя не. ГДЗ, Упр. 72, Русский язык, 6 класс, Разумовская М.М., Леканта П.А.

ГДЗ Геометрия 11 класс 10 класс Атанасян Л.С.

Пожаловаться

Елена Горлова

Найдите расстояние от точки М до плоскости АВС, если... Вопросы и задачи 143, Геометрия, 10-11 класс, Атанасян Л.С.

Добрый вечер. Не поможете решить?

Расстояние от точки М до каждой из вершин правильного треугольника АВС равно 4 см. Найдите расстояние от точки М до плоскости АВС, если АВ = 6 см.

2 ответа

Лучший ответ

Изольда Иванова

Пожаловаться

Почему же не поможем? Поможем!

Проводим
Т.к, равные наклонные имеют равные проекции, АО=ОВ=ОС=R, где R - радиус описанной окружности около ΔАВС.
По следствию из теоремы синусов:

ΔАОМ - прямоугольный, то ρ(M, (АВС)) = МО = МО = 2 см.
Ответ: ρ(M; (ABС)) = 2 см.

еще ответы

Мария Хохлова

Пожаловаться

Предлагаю ещё один способ решения:

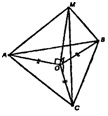
Проведем МО - перпендикуляр от М к плоскости АБС. От вершины А через точку О проведем прямую АК, пересекающую сторону треугольника БС. Так как этот треугольник равносторонний, АК будет биссектрисой, медианой и высотой. И будет делиться точкой О в отношении 2:1 от вершины.

Теперь рассмотрим треугольник АБК. Нам известна сторона АБ = 6 (по условию) и сторона БК = 3 (так как БК = половине БС, а БС по условию 6). По теореме Пифагора найдем АК. АК = корень из 27.

Теперь найдём АО. Как уже было сказано выше, АК точкой О делится в отношении 2:1 от вершины. Значит, АО:ОК = 2:1, а АО:АК = 2:3. АК = корень из 27, значит АО : корню из 27 = 2:3. Решим пропорцию и получим АО = 2/3 * корень из 27.
Теперь рассмотрим треугольник АОМ. Нам известна сторона АМ = 4 и сторона АО = 2/3 * корень из 27. Найдем МО по теореме Пифагора = 2.

Ответ: 2

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения

похожие темы