Найдите расстояние от середины отрезка до плоскости ос. Вопросы и задачи 142, Геометрия, 10-11 класс, Атанасян Л.С.

Я, я!

Рассмотрим два случая:
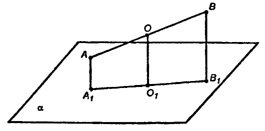
Случай I. Если АВ не пересекает а, то имеем:
АА₁ = 1 см, ВВ₁  = 4 см, О - середина АВ;
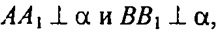то АА₁ || ВВ₁ .
Согласно аксиоме, через АА₁ и ВВ₁ можно провести единствен­ную плоскость АВВ₁А₁ .
В пл. АВВ₁А₁  проводим ОО₁ || ВВ₁ . Согласно п. 21°, т. 0 € А₁В₁
Значит, ОО₁ 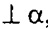ОО₁  - искомый отрезок, ρ(О, α)  = ОО₁

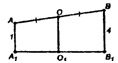
Т.о. ОО₁ - средняя линия трапеции;
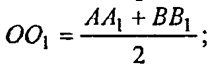ОО₁  = 2,5 см.
Случай II. АВ пересекает пл. α

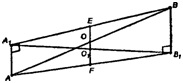
Продолжим О₁О до пересечения с А₁В и АВ₁ в точках Е и F. АО = ОВ, ОО₁ || ВВ₁ , то по теореме Фалеса AF = FB₁ .
O₁F || АА₁  по теореме Фалеса А₁О₁ = О₁В₁.
В ΔАА₁В₁ : O₁F- средняя линия, то есть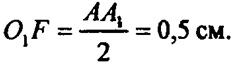 
ΔАВВ₁ : OF- средняя линия, то есть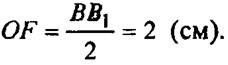 
ОО₁ = OF -  O₁F- 1,5 см.
Ответ: 2,5 см или 1,5 см (в зависимости от того, пересекает ли АВ плоскость а).