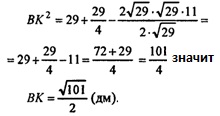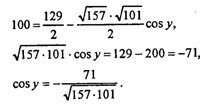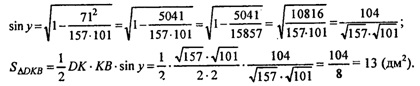Найдите площадь сечения, проведенного через диагональ. Вопросы и задачи 266, Геометрия, 10-11 класс, Атанасян Л.С.

Здравствуйте. поделюсь

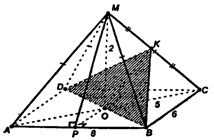
Пусть  МО  -  высота пирамиды.  Т.к.  МА =MB=MC=MD, то ОА = ОВ = ОС = OD (рав­ные  наклонные  имеют  равные проекции). Следовательно, точка О равноудалена от вер­шин прямоугольника. В пря­моугольнике таким свойством обладает точка пересечения его диагоналей, следовательно, точка О - точка пересечения диаго­налей прямоугольника.
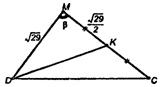
Построим сечение пирамиды плоскостью, проходящей через диагональ основания BD параллельно ребру МА.
В плоскости МОС построим OK ||МА и проведем отрезки ВК и DK.
МА||ОК, ОК с пл. DKB, следовательно, МА ||пл. DKB, ΔDKB - искомое сечение.

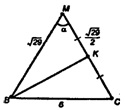
Из ΔBMC по теореме косинусов   имеем:
ВС² = МВ² +МС² - 2МВ ∙ МС ∙ cos  α,
36 = 2 ∙ 29 - 2 ∙ 29 ∙ cos а,
2 ∙ 29 cos α = 58 - 36 = 22,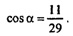 
В ΔАМС ОК - средняя линия, т.е. МК=КС. 


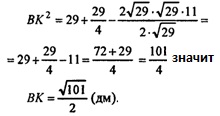
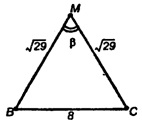
Из ΔMDC по т. косинусов имеем:
DC² = MD² + МС² - 2 ∙ MD ∙ МС ∙ cos  β,
64 = 2 ∙ 29 - 2 ∙ 29 ∙ cos β, 2 ∙ 29 ∙ cos β = -6,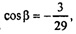 
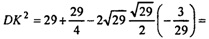
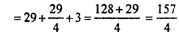, значит,


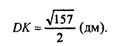
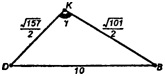
Из ΔBDK по т. косинусов имеем:
DB²  =DK²+BK²  - 2∙DK∙BK cos у,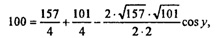 

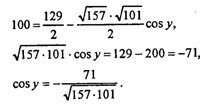
Т.к. cos²y + sin²  у = s, то

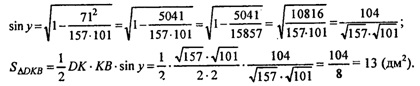
Ответ: 13 дм².