Найдите площадь сечения. Дополнительные задачи 309, Геометрия, 10-11 класс, Атанасян Л.С.

Вот чувствую прям, что эту задачку кто-то уже решил))
Основанием пирамиды с равными боковыми ребрами является прямоугольник со сторонами 6 дм и 8 дм. Высота пирамиды равна 6 дм. Найдите площадь сечения, проведенного через меньшую сторону и середину высоты.

1 ответ

Лучший ответ

Изольда Иванова

Пожаловаться

Дааааа))

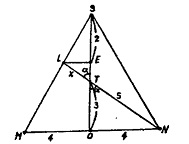
Пусть ABCDS — данная пирамида. В основании ABCD - прямоугольник, АВ=6 дм, AD=8 дм.
Построим высоту SO, SO=6 дм. Построим отрезки ОА, ОВ, ОС, OD.
По условию, боковые ребра равны. Тогда их проекции на плоскость основания тоже равны, т.е.
ОА=ОВ=ОС=ОD, и точка О — точка пересечения диагоналей прямоугольника ABCD, т.к. по свойству прямоугольного треугольника диагонали равны и в точке пересечения делятся пополам.
Построим искомое сечение.
Через точку О построим MN || AD и отрезки SM и SN. В плоскости MSN построим отрезок, соединяющий точки N и Т, где Т - середина высоты SO - и продолжим этот отрезок до пересечения с отрезком SM в точке L.
DC || АВ, значит DC || пл. ASB. Линия пересечения секущей плоскости с плоскостью ASB будет параллельна DC, то есть PQ || DC. Точки Р и D, Q и С лежат в плоскостях соответствующих граней, их соединяем отрезками PD и QC. Сечение DPQC - искомое.
Т.к. PQ || DC, то 4-угольник DPQC - трапеция.
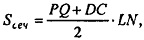т.к. LN - высота трапеции (пл. 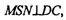а LN лежит в пл. MSN, значит;

Из ΔSON по т. Пифагора имеем:

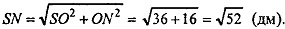
Построим 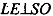Пусть LT=x.