Найдите площадь полной поверхности описанного около сферы радиуса R многогранника. ГДЗ, задача 634, Геометрия, 10-11 класс, Атанасян Л.С.

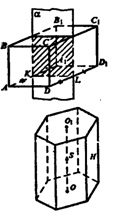
а) Рассмотрим сечение, проходящее через ось. Получим квадрат и вписанную в него окружность, ее радиус ра- вен радиусу сферы. Обозначим ребро куба через х; х = 2 R . Площадь одной грани равна х , или 4R .
Sполн=b-4R²=24R²
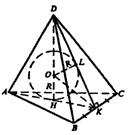
б) Высота призмы O₁O  равна  диаметру  сферы; точки касания сферы с боковыми гранями лежат в сечении призмы плоскостью, которая проходит через середину     высоты     призмы     (центр     сферы)   перпендикулярно к боковым ребрам.
Пусть сторона правильного 6-угольника равна х, тогда 

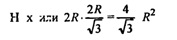
Вычислим площадь боковой поверхности:

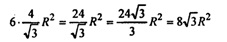
Площадь основания состоит из площадей 6-ти равносторонних треугольников, площадь каждого из которых равна 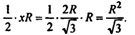Тогда площадь основания равна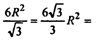 
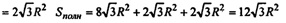
в) Все ребра тетраэдра равны; пусть они равны    х. Построим АК ┴ ВС, отрезок DK. В правильном ∆АВС АК  проходит  через  центр ∆АВС. По  теореме о трех перпендикулярах DK ┴ ВС. ∟AKD — линейный угол двугранного угла при основании тетраэдра (все двугранные углы  равны).
∆ОКL=∆ОКН, ОК — биссектриса ∟AKD.

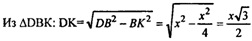
НК — радиус вписанной  окружности,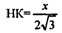 
Пусть ∟DKH= φ

Грани правильного тетраэдра — это равные равносторонние треугольники,   поэтому   плошадь   полной   поверхности   S=4∙S∆abc  24√3R2
И все чертежики