Найдите объем тетраэдра. ГДЗ, задача 743, Геометрия, 10-11 класс, Атанасян Л.С.

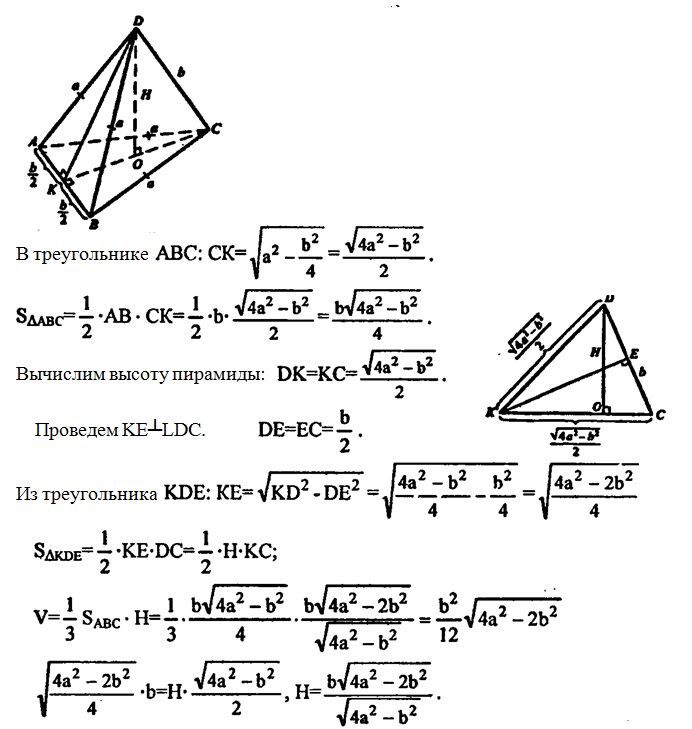
а)   Пусть   AC=AB=b,   a DA=DB=DC=BC=a.
Построим высоту пирамиды DO, отрезки ОА, ОВ, ОС.
∆doa=∆dob=∆doc.
Тогда, OA=OB=OC=R, где R — радиус окружности, описанной вокруг ∆АВС
В равнобедренном треугольнике ∆BAC проведем из угла А высоту АК.


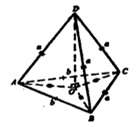
б) в равнобедренном треугольнике АВС (CA=sCB=a) построим высоту СК┴АВ; проведем отрезок DK.
В треугольнике ADB: DK — высота (∆ADB — равнобедренный, АК=КВ, значит, медиана DK является высотой).
AB┴DK, AB┴KC, AB┴(DKC).
Если плоскость  проходит  через  перпендикуляр  к другой плоскости, то она  перпендикулярна  к  этой плоскости. Итак, плоскости АВС и DKC    перпендикулярны.    В    плоскости DKC проведем высоту пирамиды DO; DO┴CK.
Примем DO=H.