Найдите cos ∟CAD. ГДЗ, дополнительные задачи 516, Геометрия, 10-11 класс, Атанасян Л.С.

CA┴AB.
Из А проведем прямую OA ┴ АВ, ∟CAO=φ.  Отложим  АС=АО;  построим отрезок СО,  из  точки  О  проведем луч, пересекающий луч AD в  точке D, OD || АВ.

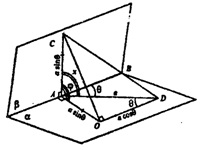
OD || АВ, а ОА ┴ АВ, значит, OD ┴ ОА. По теореме о трех перпендикулярах. CO┴OD.
Обозначим AD=a. Тогда в ∆AOD: АО=а sin θ, OD=a cos θ.
Из ∆ОАС по теореме косинусов: CO²= OA²+AC²-2∙AC∙AO*cos φ, СО²=a² sin²φ+a² sin² θ - 2a² sin² θ cos φ=2a² sin² θ (1 - cos φ).
В прямоугольном ∆COD CD²=OC²+OD²;
CD²=2 a² sin² θ (1- cos φ)+a² cos² θ.
В ∆CAD по теореме косинусов искомый ∟CAD=x, CD²=CA²+AD² - 2 CA · AD ∙ cos x.
2a²   sin²   θ (1  -  cos  φ)+a²   cos²   θ = a²   sin²   θ+a²   -2  a²   sin  θ cos    x,
2 sin² θ - 2 sin² θ cos φ+cos² θ=sin² θ+ 1- 2 sin θ cos x, 1-2 sin² θ cos φ -1=-2 sin θ cos x,
2 sin² θ cos φ=2 sin θ cos x, sin θ ≠0, следовательно, sin θ cos φ=cos x.