Найдите боковые ребра пирамиды. Дополнительные задачи 302, Геометрия, 10-11 класс, Атанасян Л.С.

Опять домашка,с которой мне не справится((
Основанием пирамиды является параллелограмм со сторонами 3 см и 7 см и одной из диагоналей 6 см. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4 см. Найдите боковые ребра пирамиды.

1 ответ

Лучший ответ

Ольга Кругло

Пожаловаться

лови готовую
Пусть ABCDS - данная пирамида. Т. О - точка пересечения диагоналей параллелограмма.

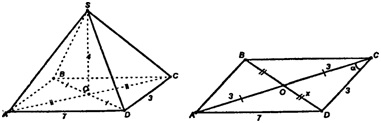
По свойству параллелограмма имеем:
BO=OD и АО=ОС.
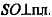ABC, SO= 4.
ΔOSB=ΔOSD (по двум катетам), тогда SB=SD;
ΔAOS=ΔCOS (по двум катетам), тогда SA=SC.
Пусть АО=ОС=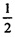АС = 3см, BO=OD=х.
Из ΔACD по теореме косинусов имеем:
AD² = АС² + CD² - 2∙АС∙CD∙cosα,
72 =62 + 32 -2∙6∙3∙cosα, 49=36+9 -36∙cosα, 36cosα = -4;

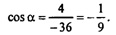
Т.к. cosα < 0, то задаче соответствует рисунок:

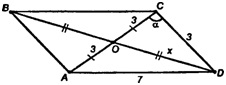
Из ΔCOD по теореме косинусов имеем:
OD² =x² = 32 + 32 - 2∙3∙3∙cosα,
х² = 9 + 9 + 2∙9∙ 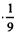= 18 + 2 = 20; х =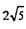(см), (т.к. х > 0)
Из прямоугольного ΔSOD по теореме Пифагора имеем:
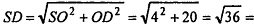6 (см), SD = SB = 6 (см).
Из прямоугольного ΔSOC по т. Пифагора имеем:
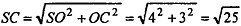= 5 см. SC = SA = 5 см.
Ответ: 5 см, 5 см, 6 см, 6 см.