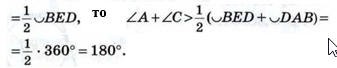ГДЗ по геометрии Атанасян 8 класс. Гл.VIII №729. Докажите, что если в четырёхугольнике сумма...

Задача Гл.VIII №729 решается так:
Пусть в четырёхугольнике ABCD
A+ C= 180°.                                       (1)
Проведём окружность через три вершины четырёхугольника: А, В и D (рис. а) — и докажем, что она проходит также через вершину С, т. е. является описанной около четырёхугольника ABCD. 
 
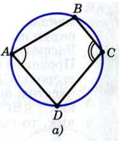
Предположим, что это не так. Тогда вершина С лежит либо внутри круга, либо вне его. Рассмотрим первый случай (рис. б). В этом случае угол C =

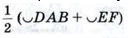
(см. задачу Гл.VIII №718), и, следовательно,

 
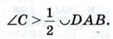
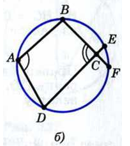
Так как А =
 
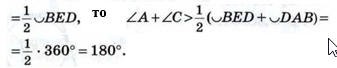
 Итак, мы получили, что углы A + C > 180°. Но это противоречит условию (1), и, значит, наше предположение ошибочно. Аналогично можно доказать (опираясь на задачу Гл.VIII №719), что вершина С не может лежать вне круга. Следовательно, вершина С лежит на окружности, что и требовалось доказать.