ГДЗ по геометрии 8 класс Атанасян. Гл.VIII №724. Докажите, что если в выпуклом четырёхугольнике...

Задание Гл.VIII №724 разобрал и доказал.
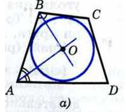
Пусть в выпуклом четырёхугольнике ABCD
АВ + CD = ВС + AD.      (1)
Точка О пересечения биссектрис углов А и В равноудалена от сторон AD, АВ и ВС, поэтому можно провести окружность с центром О, касающуюся указанных трёх сторон (рис. а). Докажем, что эта окружность касается также стороны CD и, значит, является вписанной в четырёхугольник ABCD.

Предположим, что это не так. Тогда прямая CD либо не имеет общих точек с окружностью, либо является секущей.
Рассмотрим первый случай (рис. б).
 
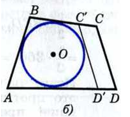
Проведём касательную C'D', параллельную стороне CD (С' и D' — точки пересечения касательной со сторонами ВС и AD). Так как ABC'D' — описанный четырёхугольник, то по свойству его сторон
AB + C'D' = BC' + AD'.          (2)
Но ВС = ВС- С'С, AD' = AD - D'D, поэтому из равенства (2) получаем:
C'D' + С'С + D'D = ВС + AD - АВ.
Правая часть этого равенства в силу (1) равна CD. Таким образом, приходим к равенству
C'D' + С'С + D'D = CD,
т. е. в четырёхугольнике C’CDD' одна сторона равна сумме трёх других сторон. Но этого не может быть, и, значит, наше предположение ошибочно. Аналогично можно доказать, что прямая CD не может быть секущей окружности. Следовательно, окружность касается стороны CD, что и требовалось доказать.