Двугранные углы при основании пирамиды равны. Вопросы и задачи 247, Геометрия, 10-11 класс, Атанасян Л.С.

Нужны помощники для решения задачи)
Двугранные углы при основании пирамиды равны. Докажите, что: а) высота пирамиды проходит через центр окружности, вписанной в основание пирамиды; б) высоты всех боковых граней, проведенные из вершины пирамиды, равны; в) площадь боковой поверхности пирамиды равна половине произведения периметра основания на высоту боковой грани, проведенную из вершины пирамиды.

1 ответ

Лучший ответ

Лена Пономарь

Пожаловаться

Я здесь! :)

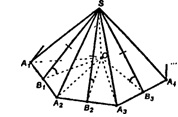
а) Пусть SO - высота некоторой n-угольной пирамиды. Построим отрез ки ОВ₁, ОВ₂, ОВ₃, ..., ОВ_n, проходящие через т. О перпендикулярно к сторонам многоугольника, лежащего в основании. По теореме о 3-х пер пендикулярах имеем: 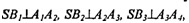и так далее, тогда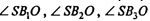
и т.д. - линейные углы двугранных углов, образованных боковыми гранями пирамиды с плоскостью основания. По условию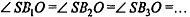
Рассмотрим ΔSOB₁, ΔSOB₂ , ΔSOB₃, и т.д. Все эти треугольники равны по катету SO и острому углу:
ΔSOB₁ =ΔSOB₂=ΔSOB₃ =... Отсюда ОВ₁=ОВ₂= ОВ₃...
Значит, точка О равноудалена от всех сторон многоугольника, лежащего в основании пирамиды, то есть является центром вписанной в многоугольник окружности.
Следовательно, высота пирамиды SO проходит через центр вписанной в основание окружности.
б) SB₁, SB₂, SB₃ и т.д. - высоты боковых граней пирамиды (по по строению). Т.к. ΔSOB₁=ΔSOB₂=ΔSOB₃=...,то SB₁= SB₂=SB₃=..
в S_ΔSA1A2=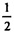A₁А₂ ∙ SB₁ , S_ΔSA2A1 =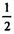А₂ А₃∙SB₂,
S_{ΔSA3 A4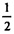} = А₃А₄ ∙ SB₃ , но SB₁=SB₂=SB₃..., следовательно,
S_бок 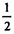А₁А₂ ∙ SB₁ +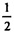А₂А₃∙SB₁ +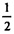А₃А₄ ∙ SB₁ +...=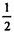SB₁(А₁А₂ + А₂А₃ +...+ А_n_1А_п + А_nА₁) =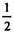SB₁ ∙ Р, где Р - периметр основания.
Р = А₁А₂ + А₂А₃ +...+ А_п_1А_п + A_nA₁.