Две секущие плоскости перпендикулярны к оси конуса... ГДЗ, задача 557, Геометрия, 10-11 класс, Атанасян Л.С.

Чертежик приложить?)

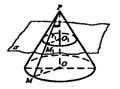
Дано: α ┴ оси конуса РО. Докажем, что
1) сечение конуса плоскостью а будет кругом с центром в точке О₁;

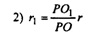
Возьмем некоторую точку Μ₁  ϵ α и точку М₁  ϵ O₁(r₁). (на плоскости а строим окружность с центром в точке O₁ и радиуса г и на этой oкружности выбираем произвольную точку М₁).
Через точку Р и точку Μ₁ проводим прямую РМ₁, которая пересечет плоскость основания конуса в точке Μ. ∆PO₁M₁~∆POM как прямоугольные, имеющие одинаковый острый угол.

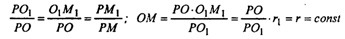
при заданной точке Р и окружности O₁(r₁).
Тогда: точка М — произвольная, значит, все точки луча РМ₁, пересекающие плоскость основания конуса, лежат на окружности О(r), т.е. равноудалены от некоторой точки О на расстояние г, что видно из формулы РМ — образующая конуса по определению.
4) Образующие составляют коническую  поверхность,  поэтому  докажем,  что   существует   произвольная   точка   M₁    ϵ   а,   M₁     ϵ   РМ   такая,   что     М ϵ О₁(r₁).
5) ∆PO₁M₁ ~ ΔΡΟΜ (РМ — образующая).
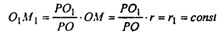при заданной точке Р и r
Тогда  эта  окружность  будет  сечением  боковой  поверхности,  а  круг, границей которого является O₁  (r₁  ), будет сечением конуса плоскостью а