Докажите, что все вершины данных прямоугольников лежат на одной сфере. ГДЗ, дополнительная задача 624, Геометрия, 10-11 класс, Атанасян Л.С.

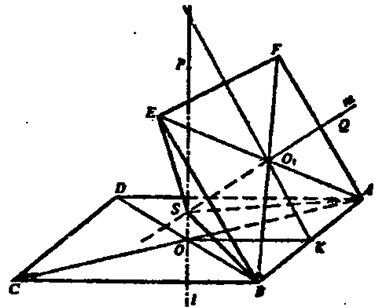
Через точку пересечения диагоналей прямоугольника ABCD проведем прямую Ɩ, Ɩ перпендикулярна плоскости ABCD. Все точки на прямой Ɩ равноудалены от вершин А, В, С, D. (Если наклонные, проведенные из одной точки, имеют равные проекции, то сами наклонные равны РА= РВ = PC = PD, P ϵ Ɩ.)
Построим отрезок OK ┴ AB,  через  точку O1 проведем луч КО₁. AB ┴ плоскости РОК.
Прямая А В лежит в плоскости прямоугольника ABEF АВ, значит плоскости РОК и ABEF взаимно перпендикулярны. Проведем через точку Ο₁ прямую т ┴ плоскости ABEF.
Если две плоскости перпендикулярны и к одной из них проведен перпендикуляр, который имеет общую точку с другой плоскостью, то этот перпендикуляр принадлежит в этой плоскости.
Таким образом, т с плоскости РОК; т геометрическое место точек, равноудаленных от вершин прямоугольника ABEF: QA = QB = QE = QF Q ϵ m. Прямые Ɩ и т пересекаются в точка S, которая равноудалена как от вершин прямоугольник ABCD, так и от вершин прямоугольника ABEF.
Докажем, что точка S равноудалена от вершин А, В, С, D и вершин E, F
Проведем отрезки SA, SE, SB.
∆SAO₁ = ∆SOB (они прямоугольные, SO — общий катет, ОА = ОВ по свойству диагоналей прямоугольника).
Отсюда SA = SB. Значит, SA =SB = SE
Доказано, что SA = SB = SE = SC = SD и SA = SB = SE = SF, следовательно, точка S равноудалена от всех вершин, значит, она является центром сферы, проходящей через все данные вершины.