Докажите, что при параллельном переносе на вектор... ГДЗ, дополнительные задачи 520, Геометрия, 10-11 класс, Атанасян Л.С.

Лови вместе с чертежами!
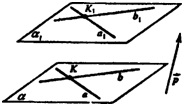
а) Возьмем в плоскости а точку К и проведем через нее две пересекающиеся прямые а и b. При параллельном переносе прямая b перейдет в параллельную  ей  прямую b1,  а  прямая  а  —  в  параллельную  ей прямую a₁. Т.к. а и b пересекаются, то  а₁ и  b₁   тоже  пересекаются.  Через  a₁ и b₁   проведем  плоскость  а.  Если  две  пересекающиеся  прямые  одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны. Тогда, а|| а₁ что и требовалось доказать.

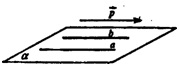
б) проведем на плоскости а прямую ā  ||  р  и  b  ||  р.  Известно,  что прямая, параллельная р или содержащая р, отображается на себя. b  →  b,  а  →  а .  Через  параллельные прямые а и b проходит единственная плоскость а, которая таким образом отображается сама на себя, что и требовалось доказать.