Докажите, что при осевой симметрии... ГДЗ, вопросы и задачи 481, Геометрия, 10-11 класс, Атанасян Л.С.

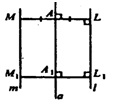
а)  Пусть  а  —  ось  симметрии,  Ɩ  ||  α.  Из  точки L ϵ Ɩ проведем LA┴a; продолжим LA за точку А на расстояние AM=LA.
Из точки L₁  ϵ  Ɩ  проведем  L₁A₁┴a;  продолжим  L₁A₁ за точку A₁ на расстояние A₁M₁ = L₁A₁.
Параллельные    прямые    а    и    Ɩ    лежат    в  одной плоскости, тогда четырехугольник LMM₁L₁ - плоский четырехугольник.
ML=M₁L₁ — по построению, ML┴ Ɩ, M₁L₁┴ Ɩ, следовательно, ML||M₁L₁ поэтому четырехугольник LMM₁L₁  — прямоугольник. Т.е.,
MM₁||L₁L, или Ɩ ||m.
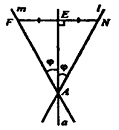
б) Если а не параллельна Ɩ, то а пересекается с L в некоторой точке А.
Выберем некоторую точку N ϵ Ɩ, построим NE┴a, продолжим отрезок NE за точку Е на расстояние EF=NE. Через точку F проведем прямую FA (m).
В треугольниках ∆AEF и ΔΑΕΝ. NE=EF, АЕ - общий катет, таким   образом,
∆AEF=∆AEN, следовательно, ∟EAN=∟EAF=φ.
Таким образом, прямая m образует угол φ с осью симметрии.