Докажите, что при движении происходит следующее... ГДЗ, вопросы и задачи 487, Геометрия, 10-11 класс, Атанасян Л.С.

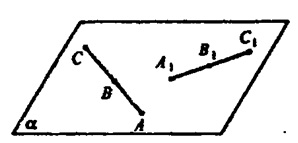
а) АС — заданный отрезок, АС с а.
При движении А → А₁, С →С₁. Докажем, что весь отрезок АС отображается на отрезок A₁C₁.
Возьмем произвольную точку В ϵ АС. При движении В → В₁. АВ+ВС=АС. Т.к. при движении расстояния между точками сохраняются, то A₁B₁=AB, B₁C₁=BC, A₁C₁=AC. Тогда A₁C₁=A₁B₁+B₁C Равенство выполняется только когда точки А₁, B₁, C₁ лежат на одной прямой, иначе по неравенству треугольника A₁C₁ < A₁B₁+B₁C₁, таким образом, точки отрезка АС отображаются в точки отрезка A₁C₁.
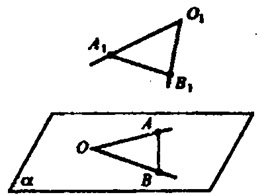
б) ∟АОВ — лежит в плоскости а.
При движении О → О₁, Α→Α₁, В→В₁ при этом ΟΑ=Ο₁Α₁ и OB=O₁B₁ AB=A₁B₁ и ΔΟΑΒ = Δ O₁A₁B₁ по трем сторонам, тогда ∟AOB=∟A₁B₁C₁. Если ∟АОВ=180°, то ∟A₁O₁B₁=180°.
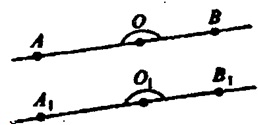
Доказательство:
На  сторонах  развернутого  угла  возьмем  течки  А  и  В.  При       движении A→A₁, B→B₁, так что ΑΒ=Α₁Β₁, так что ΑΒ=Α₁Β₁; O→O₁ при движении AO=A₁O₁ и Ο₁Β₁=ΟΒ. Итак, AO₁+O₁B₁=A₁B₁.
Точки A₁, Ο₁, B₁ лежат на одной прямой, точки  A₁ и В₁ лежат по разные стороны от точки  О₁,  тогда,  ∟A₁O₁B₁    —  развернутый,  т.е.  Δ Α₁Ο₁Β₁ = 1800, что и требовалось доказать.