Докажите, что при центральной симметрии верны утверждения.... ГДЗ, вопросы и задачи 480, Геометрия, 10-11 класс, Атанасян Л.С.

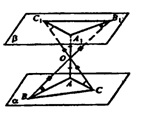
а) Пусть О — центр симметрии, а — данная плоскость.
1.  Пусть точку Сϵа, построим отрезок СО и продолжим его за точку О на расстояние OC₁ = ОС.
2.  Пусть точка Аϵа, построим отрезок АО и продолжим его за точку О на расстояние OC₁=OA.
3.   Пусть точка Bϵа, построим отрезок ВО и продолжим его за точку О на расстояние OB₁=OB.
4.  Через точки A₁, В₁, С₁ проведем плоскость β.
5.    Соединим точки А, В, С, А₁, B₁ и C₁ отрезками.    ∆ОАС=∆O₁А₁С₁ т.к. OA₁=OA, OC₁=OC и ∟AOC=∆A₁OC₁ как вертикальные.
Отсюда АС =А₁С₁.
Тогда ∟A₁C₁O=∟ACO, по признаку параллельности прямых A₁C||AC.
6.  Для ΔΟΑΒ и ΔΟΑ₁Β₁ проведем аналогичные рассуждения и получим, что ΔΟΑΒ=ΟΑ₁Β₁. Тогда ∟A₁B₁O=∟ABO, по признаку параллельности прямых Α₁Β₁||ΑΒ.
7.  Если две пересекающиеся прямые (АС и АВ) в одной   плоскости (а)  соответственно параллельны двум прямым (A₁C и A₁B₁) другой плоскости (β), то эти плоскости параллельны. Итак, α||β,утверждение доказано.
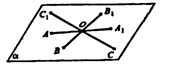
б) Если точка О ϵ α, то любая точка плоскости β имеет симметричную ей точку относительно О, тоже принадлежащую плоскости α.
Тогда для А ϵ а ей симметричная точка A₁ ϵ α; для В ϵ α ей симметричная точка B₁ ϵ α; для С ϵ α ей симметричная точка C₁ ϵ α.
Через три точки A₁, В₁, С₁ принадлежащие плоскости β, можно провести единственную плоскость, соответственно, она совпадает с плоскостью α.