Докажите, что при центральной симметрии... ГДЗ, вопросы и задачи 479, Геометрия, 10-11 класс, Атанасян Л.С.

Привет!
а) По известной теореме через центр симметрии и данную плоскость можно провести единственную плоскость.

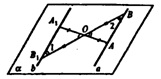
Пусть О — центр симметрии, а—данная прямая, а —плоскость, проведенная через О и a
Пусть А ϵ а, построим отрезок ОА.
Продолжим ОА за точку О на расстояние OA₁=AO. Получим точку А₁, симметричную А.
Пусть В ϵ а, построим отрезок ОВ. Продолжим ОВ за точку О на расстояние OB₁=OB. Получим точку В₁, симметричную точке В.
Через A₁  и B₁  проведем прямую b. Рассмотрим ∆AОВ и    ΔΑ₁ΟΒ₁·ΑΟ=Α₁Ο, ВО=ОВ₁, Δ ΑΟΒ=ΔΑ₁ΟΒ₁ как вертикальные, следовательно, ΔΑΟΒ=ΔΑ₁OΒ₁.
Тогда, ∟1=∟2 и а || b.
б) Пусть А ϵ а. Симметричная ей точка A₁ тоже принадлежит прямой а;АО=ОА₁.

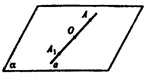
Точка  А  произвольна,  следовательно,  любая точка прямой, а также симметричная точка относительно центра О лежат на прямой а, следовательно, прямая а переходит сама в себя при условии, что проходит через центр симметрии.