Докажите, что полученная фигура - параллелепипед. Вопросы и задачи 78, Геометрия, 10-11 класс, Атанасян Л.С.

Поделитесь решением, кому не жалко!!!!

На рисунке изображен параллелепипед АВСDА₁В₁С₁D₁, на ребрах которого отмечены точки М, N, М₁ и N₁ так, что АМ = СN = А₁М₁ = С₁N₁. Докажите, что МВNDМ₁В₁N₁D₁ — параллелепипед.

1 ответ

Лучший ответ

Ринка-Ринка

Пожаловаться

Делюсь
ABCD- параллелограмм по условию, АВ = CD. AB-AM=CD-CN , то есть ВМ= DN.
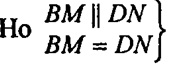→ по признаку параллелограмма,
MBND - параллелограмм.
Аналогично получим, что N₁B₁M₁D₁ - параллелограмм.
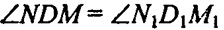- как углы с соответственно параллельными и одинаково направленными сторонами.
Параллелограммы MBND и M₁B₁N₁D₁ равны, так как равны их соответствующие стороны (МВ = М₁В₁ , M₁D₁ = MD) и угол между ними (п. 5).
А₁М₁ =АМ , поэтому А₁М₁МА - параллелограмм, М₁М || А₁А || В₁В.
Аналогично, C₁NN₁C - параллелограмм, С₁С || NN₁ || DD₁ .
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны, поэтому
ММ₁ = ВВ₁ = СС₁ = NN₁ = DD₁ .
По признаку параллелограмма 4-угольники DNN₁D₁ и MDD₁M₁ - параллелограммы.
По определению (п. 13) MBNDM₁B₁N₁D₁ - параллелепипед.