Докажите, что отрезки пересекаются в одной точке. Дополнительные задачи 108, Геометрия, 10-11 класс, Атанасян Л.С.

Приветик, у меня есть решение))

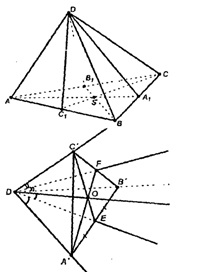
Отложим от т. D на ребрах DA, DB,  DC равные отрезки:  DA' =  DB′ = DC′ = а. Соединим точки А′, В′ и С′ отрезками. Нарисуем ограниченную этими отрезками  часть  тетраэдра,  для удобства «положив» его на одну из боковых граней.
Проведем биссектрисы двух уг­лов при вершине D: DE и DF; про­ведем отрезки С′Е и A′F.
В ΔА'DB' DA' = DB′ и DE является медианой, следовательно, ЕА′ = В'Е (т.к. Δ А′DB' равнобедренный).
В ΔС′DB′ DF - общая, DC′ = DB′, 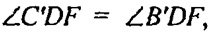 поэтому ΔC′DF =ΔB′DF, следовательно, C′F=F′B.
В ΔА′В′С′ отрезки С'Е и А′F являются медианами 
Чтобы на загромождать рисунок, не показана биссектриса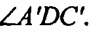 
Если для нее повторить рассуждения, то убедимся, что от­резок, исходящий из В' в точку, где биссектриса пересечет сторону А'С' будет третьей медианой в ΔА'В'С'. А три медианы треугольни­ка пересекаются в одной точке.
Таким образом, плоскости DEC', DFA' и третья, не показанная на рисунке, пересекаются на рисунке по прямой DO.
Уберем ограничение, что DA' = DB' = DC'. Факт, что плоскости пересекаются по прямой DO, останется верным.
Равные отрезки от вершины D можно отложить в любом тетраэдре, поэтому на строгость (или общность) доказательства это по­влиять не может.
Раз указанные плоскости пересекаются по прямой DO, то эта прямая пересечется с плоскостью основания в некоторой точке, зна­чит, все три отрезка АА₁, CC₁  и ВВ₁  проходят через нее.
Что и требовалось доказать.