Докажите, что каждая координата суммы (разности) двух векторов равна... Вопросы и задачи 406, Геометрия, 10-11 класс, Атанасян Л.С.

Рассмотрим  общий  случай.

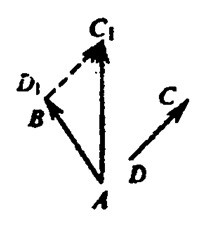
Рассмотрим  два  некомпланарных вектора АВ и DC. Перенесем вектор DC параллельно так, чтобы точка D₁ его начала совпала с точкой В конца первого вектора. Получим вектор D₁C₁ или, что то же самое, вектор ВС₁, сонаправленный с вектором DC и равный ему по длине. Согласно правилу сложения векторов: AB+DC=AB+BC₁=AC_I.
Пусть AB {x1; у1; z1}, ВС₁ {х2; у2; z2}. Докажем, что  АС₁ {х1+х2, у1+у2; z1+z2}.
Для доказательства  выразим координаты  этих векторов через    координаты их начала и конца. АВ (хв  - хА; ув  - уА; zΒ  - zα), ВС₁ { xс1 - xB, yс1 - yв, zc1,- zв}, АС₁ { xс1 - хА; ус1 - yA, zc1 - z.а}, из обозначения координат вектора АВ как x1, y1 и z1 и вектора ВС₁ как х2, у2, z2, получим Х1=хв-Ха, У1=Ув - Уа, z1=zb - za, x2= xc1 - xВ, у2= ус1 - yв, z2= zc1 - zB.
Вычислим суммы Χ1+X2, У1+У2, Z2+Z2. x1+x2=xB-xa+xC1 -xВ=xС1 —xA,
y1+y2=yB  - yа+yс1-yв=yс1-yа. z2+z2=zb  - zΑ+zC1-zΒ=zC1-zΑ,
Суммы координат  х1+х2,  y1+y2,  z2+z2  являются  координатами  вектора АС), равного сумме исходных двух векторов АВ и DC. Что и требовалось доказать.