Докажите, что центры граней правильного октаэдра являются... Дополнительные задачи 315, Геометрия, 10-11 класс, Атанасян Л.С.
вот так
Правильный октаэдр состоит из 8 равносторонних треугольников.
ABCD - одна из плоскостей симметрии. Выполним построение для верхней половины октаэдра, тогда построение для нижней части есть зеркальное отображение построения в верхней части. Совместим половины октаэдра и получим полное построение.
ABCD - квадрат, все боковые грани равные между собой равносторонние треугольники. Возьмем грани: ΔАВЕ и ΔADE. Центром равностороннего треугольника является точка пересечения медиан, высот и биссектрис.
Пусть L и К - такие точки для граней ΔАВЕ и ΔADE (соответственно). Построим проекции L и К на ABCD. Пусть это будут точки М и N (соответственно). Аналогично простроим проекции двух других центров боковых граней на ABCD.
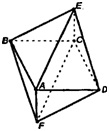
Итак, мы построили многогранник, докажем, что он - прямо угольный параллелепипед.
Центры противоположных боковых граней лежат в плоскостях, проходящих через середины противоположных сторон квадрата ABCD и вершину Е. Эти плоскости взаимно перпендикулярны. Т.о. четырехугольники, являющиеся основаниями полученного многогранника, имеют взаимно перпендикулярные диагонали, т.е. они или ромбы, или квадраты.
Т.к. грани АВЕ и AQE одинаково наклонены к плоскости основания, то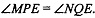 
ΔPLN=ΔQKN (прямоугольные, равны по 2-му признаку).
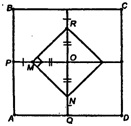
Из равенства треугольников имеем: PM=NQ.
ОМ = ON. Все четыре прямоугольных треугольника равны, следовательно,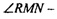 
прямой. Отсюда имеем, что основания - квадраты.
Боковые грани многогранника также прямоугольники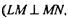 
LK || MN).
Докажем теперь, что полученный многогранник - половина куба, т.е.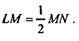 
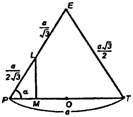
Пусть сторона основания пирамиды - а.
Построим сечение верхней половины октаэдра плоскостью, проходящей через вершину Е и середины противоположных сторон квадрата.
Из ΔВРЕ: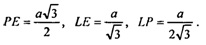 
По т. косинусов из ΔРЕТ имеем:
Совместим зеркальное построение для нижней половины и получим куб с ребром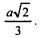 
Вывод: центры граней правильного октаэдра есть вершины куба.
