Докажите, что центры граней куба являются вершинами правильного октаэдра. Дополнительные задачи 317, Геометрия, 10-11 класс, Атанасян Л.С.

Привет. Лови свой ответ
Т.к. плоскость MNKL является плоскостью симметрии куба, то достаточно привести доказательство для верхней части многогран­ ника, расположенного внутри него.

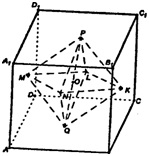
Построим ось симметрии PQ, и произведем поворот тетраэдра PMNLK вокруг РО. Тогда на место ΔNPK перейдет ΔMPN, a ΔNPK =ΔMPN, ΔMPN встанет вместо ΔKPL, который тоже равен ему, и так далее. Т.к. AMPN = АМРК = AKPL = ALPM, то МР = КР = LP = NP и MN= MK = KL = LM. PM = MN, т.к. это расстояние между смежны­ми гранями куба. Т.е. для верхней половины многогранника получим, что он составлен из 4-х равных равносторонних треугольников, в си­лу симметрии имеет место аналогичное утверждение и для нижней части, следовательно, многогранник составлен из 8 равных равносто­ронних треугольников, т.е. является октаэдром по определению.