Докажите, что центр сферы, описанной около... ГДЗ, задача 637, Геометрия, 10-11 класс, Атанасян Л.С.

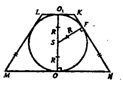
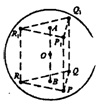
а) В основаниях призмы лежат равносторонние треугольники. Пусть А и В   —   центры оснований.
Все точки, которые лежат на перпендикуляре, проведенному через точку В к верхнему основанию призмы равноудалены от вершин треугольника PQR.
Все точки, которые лежат на перпендикуляре, проведенному через т. А, к верхнему основанию призмы, равноудалены  от  вершин  ∆P₁Q₁R₁.  Т.к. призма правильная, то  треугольники  P₁Q₁R  и  PQR  проектируются  один на другой, следовательно, точка В проектируется в точку А и обратно. Поэтому, АВ ┴ плоскости PQR. Тогда, отрезок АВ является геометрическим местом точек, равноудаленных от вершин каждого из треугольников. А его середина  —  точка  О  —  равноудалена  от  вершин  ∆P₁O₁R₁ и  от вершин ∆PQR на расстояние R, равное радиусу описанной около призмы сферы.
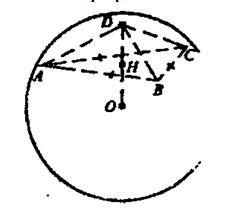
б) Построим из вершины D пирамиды высоту DH ┴ плоскости АВС. Проведем отрезки НА, НВ, НС.
∆DНА=∆DНВ=∆ОНС (они прямоугольные, DH  — общий катет, AD=BD=BC — по условию).
НА=НВ=НС=r r — радиус описанной около Δ АВС окружности.
Проведем отрезок OG┴ плоскости АВС (точка G на рисунке не показана). Проведем отрезки GA, GB, GC, ОА, ОВ, ОС,
∆DCA=∆OGB=∆OGC (катет OG — общий, ОA=ОВ=OС —R, R — радиус сферы). Значит, GA=GB=GC=r, r— радиус окружности, описанной около ΔΑΒΟ Следовательно, вокруг ∆АВС можно описать единственную окружность.
Точки Н и G совпадают, и точки D, Н, О лежат на одной прямой. Следовательно,  центр  сферы  О  лежит  на  высоте   пирамиды DH или на продолжении за точку Н, что и показано на рисунке.