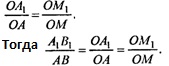Докажите, что боковые ребра и высота пирамиды делятся... Вопросы и задачи 267, Геометрия, 10-11 класс, Атанасян Л.С.

Есть, но мало))

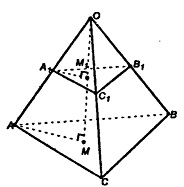
Если в основании пирамиды лежит многоугольник, то его можно всегда разбить диагоналями  на  треугольники,  и значит, n-угольная пирамида будет состоять из многих треугольных пира­мид. Докажем данное свойство для треугольной пирамиды.
Пл. A₁B₁C₁  || пл. АВС.
Линии    пересечения   двух    параллельных плоскостей третьей - параллельны, следовательно, A₁C₁ || АС, B₁C₁ || АВ, С₁ B₁ || СВ, и ΔОА₁С₁ ~ ΔOAC, следовательно,

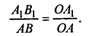
Пусть ОМ - высота пирамиды.
Прямоугольные треугольники А₁ОМ₁ и AОМ подобны по обще­ му острому углу при вершине О, значит,

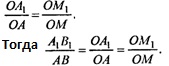
Т.к. утверждение доказано для одной произвольно выбранной грани, то пропорциональность частей, на которые плоскость делит высоту и боковые ребра других граней, остается в силе.