Докажите, что β1 совпадает с β. ГДЗ, вопросы и задачи 483, Геометрия, 10-11 класс, Атанасян Л.С.

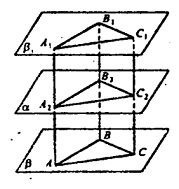
а)  Выберем  три  точки  в  плоскости  А,  В,  С,  не  лежащие  на одной прямой. Проведем AA₂┴α, ВВ₂┴α,  СС₂┴α.  Продолжим  эти отрезки  за  точки А₁, В₁, C₁ так, что A₂A₁=AA₂, B₂B₁=BB₂, C₂C₁=CC₂. AA₁B₁B — прямоугольник, т.к. AA₁=BB₁ и АА₁||| BB₁. Таким образом, A₁B₁|||AB BB₁C₁C — прямоугольник, т.к. BB₁=CC₁ и BB₁|| ВС тогда, В₁С₁  || ВС.
Плоскость β₁  проходит через точки A₁, В₁ и С₁ она — единственная.
Если две пересекающиеся прямые  (ВА  и  ВС)  одной  плоскости  (β)  параллельны  двум прямым (B₁A₁ и В₁С₁) другой плоскости (β₁),  то  эти  плоскости параллельны: β₁  || β.
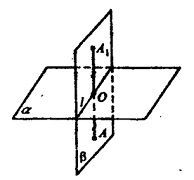
б) Пусть α┴β. Возьмем произвольную точку А ϵ α и построим АО пер- пендикулярно плоскости α. Продолжим отрезок за точку О на расстояние ОА₁=АО
Две   плоскости   взаимно   перпендикулярны   и  к одной из них проведен перпендикуляр, имеющий общую точку с другой плоскостью, тогда этот перпендикуляр весь лежит в этой плоскости, т.е. АОсβ, следовательно, и АА₁cβ
Таким образом, каждая точка плоскости β отображается в точку, ей симметричную, которая гоже принадлежит плоскости в. тогда, плоскость β отображается сама на себя, или β₁ совпадает с β.