Докажите §7 №38 ГДЗ Геометрия 7-9 класс Погорелов А.В.

1)     Надо доказать, что если расстояние между центрами окружности 20 см, а радиусы 8 см и 11 см, то окружности находятся одна вне другой.
 
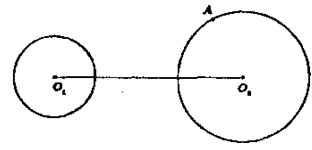
Примем О1, O2 — центры окружностей, a R1, R2 — их радиусы; O1О2 = 20 см, R1 = 8 см, R2 = 11 см.
Допустим, что эти окружности имеют общую внутреннюю точку А, следовательно O1А ≤ R1, O2A ≤ R2. Так как для любых трех точек расстояние между любыми двумя из них не больше суммы расстояний от них до третьей точки, то O2O1 ≤ О1А+O2А, O1O2 ≤ R1+R2 так как 01А ≤ R1, O2А ≤ R2 Получим 20 ≤ 8 + 11, 20 ≤19, что неверно, а значит, окружности не имеют общих внутренних точек и лежат одна вне другой.
2)       Надо доказать, что если О1O2 = 5 см, a R1 = 6 см, R2 = 12 см, то окружность с центром О1 и радиусом R1, находится внутри второй окружности с центром O2 и радиусом R2.
 
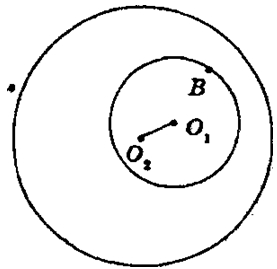
Первая окружность находится внутри второй, если, все точки, первой окружности являются внутренними точками второй окружности.
Предположим, что существует точка В на первой окружности, которая лежит вне второй окружности.
Следовательно ВО1 = R1; ВО2 > R2 ВО1 = 6 см; ВО2 > 12 см.
По неравенству треугольника для точек В, О1, O2 получим: ВО2 ≤ ВО1 + О1О2;
ВO2≤6 + 5;
ВО2≤ 11 см.
Получили противоречие (ВО2 > 12; ВO2 ≤ 11). Значит, все точки первой окружности являются внутренними точками второй окружности, то есть первая окружность лежит внутри второй.