Докажите §7 №22 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Пусть дана окружность с центром О и радиусом R и прямая а, отстоящая от центра на расстояние h < R.
Так как R > h, то из точки О можно провести две и только две наклонные длиной R (см. задачу № 21 § 7). Обозначим эти наклонные OC1 и ОС2. Так как OC1 = ОС2 = R, то точки С1 и С2 лежат на окружности с центром О и радиусом R. А значит, прямая а имеет с окружностью две общие точки. В задаче № 14* § 5 было доказано, что окружность и прямая не могут иметь более двух общих точек

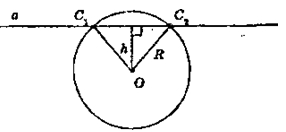
Значит, если расстояние от центра окружности до прямой меньше радиуса, то прямая пересекает окружность в двух и только двух различных точках. Что и требовалось доказать.