Будет ли пирамида правильной? Вопрос №9 к 3 главе, Геометрия, 10-11 класс, Атанасян Л.С.

Мое вот:
Рассмотрим простейший случай: пирамида треугольная.

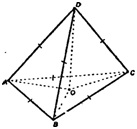
Пусть ΔADВ — правильный, AD=a. То­ гда по условию ΔBDC и ΔA DC - тоже пра­вильные треугольники со сторонами, равными а. Значит, ΔADC=ΔBDC=ΔADB. 
Построим высоту пирамиды DO. DO┴пл. АВС. Построим отрезки ОА, ОВ, ОС.
ΔDOA=ΔDOB=ΔDOC (по катету DO и гипотенузам DA = DB = DC), тогда из равенства треугольников следует: ОА=ОВ=ОС, точка О - центр пра­вильного ΔАВС. По определению пирамида DABC - правильная.
Когда  пирамида  имеет я граней и все они правильные треугольники, то все рассуждения аналогичны. а) Все боковые грани равны.
б) Построим высоту пирамиды, основание высоты - точка О. Соединяем т. О с вершинами n-угольника, лежащего в основании.
Получили л прямоугольных треугольников, которые равны по катету  и гипотенузе. Значит, равны и отрезки, соединяющие т. О с вершина­ми  n-угольника.  Следовательно,  т. О равноудалена  от вершин n-угольника, следовательно, является центром правильного n-угольника. 
По определению данная пирамида - правильная.
Ответ: будет.