Стороны треугольника. Задача 338 § 4 глава 4 Геометрия 7-9 класс Атанасян Л.С.
Мы прямо в классе эту задачу решали так:
Рассмотрим треугольник АВС, пусть сторона АС является наибольшей стороной ∆ АВС. Пусть DЕ - отрезок с концами на разных сторонах треугольника АВС
Не ограничивая общности достаточно рассмотреть два возможных расположения отрезка DЕ:
1) Один из концов отрезка лежит на наибольшей стороне треугольника (см. рисунок).
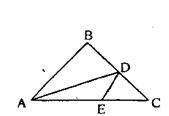
Если отрезок соединяет вершину треугольника с точкой, лежащей на противоположной стороне, то этот отрезок меньше большей из двух других сторон (см. задачу №312).
В ∆АВС AD- отрезок, соединяющий вершину треугольника с точкой, лежащей на противоположной стороне, а сторона АС - наибольшая сторона ∆ АВС, следовательно, AD<AC.
Теперь рассмотрим ∆ADC, DE- отрезок, соединяющий вершину
треугольника с точкой, лежащей на противоположной стороне, зна
чит, DE≤ADили DE≤DC, но AD<AC(по доказанному) и
DC≤BC<AC(так как АС - наибольшая сторона ∆АВС), следова-
тельно, ОЕ<АС.
2) Ни один из концов отрезка DЕ не ле жит на наибольшей стороне треугольника (см. рисунок).
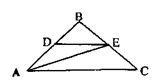
В ∆ АВС АЕ - отрезок, соединяющий вершину треугольника с точкой, лежащей на противоположной стороне, значит, АЕ<АС, т.к. АС - наибольшая сторона ∆ АВС.
Теперь рассмотрим ∆АЕВ, DE- отрезок, соединяющий вершину треугольника с точкой, лежащей на противоположной стороне, значит, DЕ≤АЕ или DЕ≤ВЕ, но АЕ<АС (по доказанному) к ВЕ≤ВС<АС (так как АС - наибольшая сторона ∆АВС), следовательно, DЕ<АС. Что и требовалось доказать.
