Стороны многоугольника. Задача 361 § 1 глава 5 Геометрия 7-9 класс Атанасян Л.С.

Всем бодренького дня, вот какое решение будет по этой задаче:
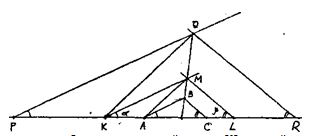
Проводим прямую. Откладываем на ней отрезок КL, равный периметру треугольника. Строим известные углы с вершинами в точках К и L. Находим пересечение их сторон — точку М. От точки К откладываем на исходную прямую отрезок, равный КМ, находим т Р. Аналогично находим т .R. через т. Р проводи прямую, параллельную КМ, через т. Q — параллельную LМ. Их пересечение — т. Q Проводим прямую QМ, а также соединяем Q и К. Через точку М проводим прямую, параллельную КQ, находим т.А, через нее проводим прямую, параллельную КМ до пересечения с ОМ, находим т. В. Через нее проводим прямую, параллельную LМ, => т. С. Из подобия треугольников АВС, КLМ и РQR получаем, что АВ = АК, ВС = СL т.е. АВ + ВС + АС = КL, т.е. ∆АВС — искомый.