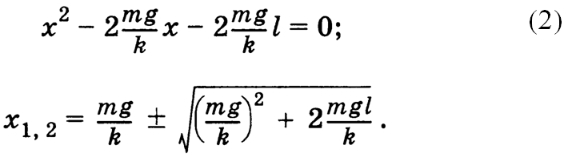Разорвется ли леска № 372 ГДЗ Рфизика 10 класс Рымкевич А.П.

Рассмотрим положение груза перед падени-
ем в нижней точке, соответствующей максимальному
растяжению х лески (если, конечно, она не порвется).
Поскольку в нижней точке скорость груза равна ну-
лю, закон сохранения энергии можно записать в виде

Здесь l — исходная длина лески, k — ее жесткость.
Левая часть уравнения (1) описывает энергию систе-
мы в начальном положении при условии, что потен-
циальная энергия груза в поле тяжести отсчитывает-
ся от нижней точки его падения. Правая часть (1)
описывает потенциальную энергию растянутой ле-
ски. Уравнение (1) — это квадратное уравнение отно-
сительно параметра х. Решая его, мы находим воз-
можное максимальное натяжение лески:

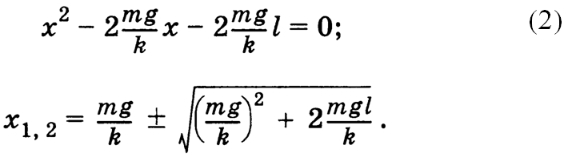
Зная эту величину, можно определить максимальную
силу упругости. Согласно закону Гука
Fупр = kx.

Таким образом, х ≈ 0,2 м, поскольку лишь положи-
тельные корни уравнения (2) имеют смысл.
Fупр = 2500 Н/м ∙ 0,02 м ≈ 50 Н.
Как мы видим, эта величина превышает заданную
прочность лески. Отсюда мы делаем вывод, что груз
не достигнет нижней точки вообще, поскольку нить
порвется.
Ответ: разорвется, так как возникшая сила упругости
равна 50 Н.