Равенство треугольников. Дополнительная задача 176 § 4 II глава Геометрия 7-9 класс Атанасян Л.С.

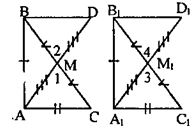
Дано: АВ=А1B1, АС=А1С1
АМ, А1М1 — медианы
АМ=А1М1
Доказать: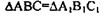 
Доказательство.
1) дополнительное построение: проведем АМ и А1М1 за точки
МиМ1и отметим на продолжениях точки D и D1 чтобы АМ=АD, А1М1=М1D1
2) Рассмотрим 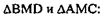АМ=МD, ВМ=МС,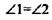  
т. к. они вертикальные, значит по 1-му признаку, следовательно, АС=ВD следует из АС=А1С1, ВD=В1D1,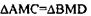 
Рассмотрим: А1М1=М1D1, значит В1М1=М1С1,
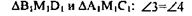т.к. они вертикальные,
значит ∆А1М1С1=∆В1М1D1 по 1-му признаку, следовательно,
А1С1= В1D1
1) Рассмотрим ∆А1B1D1 и ∆АВD:
АВ=А1B1, АD=А1D1 следует из АМ=А1М1, BD=B1D1 значит ∆АВD=∆А1B1D1, т. е. медианы ВМ и В1М1 треугольников опущены на соответственно равные стороны АD и А1D1,
Из ВМ=В1М1, следует ВС=В1C1, т.к. (ВC=2ВМ; В1С1=2В1M1).
2) Рассмотрим ∆А1В1С1 и ∆АВС:
АВ=А1В1, АС=А1C1.
Имеем: ВС= В1С1, значит ∆АВС=∆А1B1С1 по 3-му признаку, что и требовалось доказать.