Расположение точек на прямой. Дополнительная задача 221 § 2 III глава Геометрия 7-9 класс Атанасян Л.С.

Всем привет. Помогите пожалуйста с задачей?
Даны треугольник АВС и точки М и N такие, что середина отрезка ВМ совпадает с серединой стороны АС, а середина отрезка CN— с серединой стороны АВ. Докажите, что точки М, N и А лежат на одной прямой.

1 ответ

ответы

Варвара

Пожаловаться

Привет, вот ответ

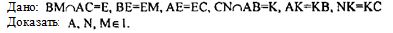
Доказательство:
Рассмотрим ∆ВСК и ∆АКN: АК=КВ.
Имеем: NК=КС, 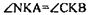т.к. они вертикальные, значит
∆АKN=∆ВСК по 1-му признаку, следовательно,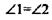
Рассмотрим ДВЕС и ДАЕМ: МЕ=ЕВ.
Имеем: АЕ=ЕС, 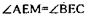- как вертикальные значит
∆АЕМ=∆ВЕС по 1-му признаку равенства Д.
Следовательно 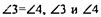- накрестлежащие углы при пря-
мых АМ и ВС и секущей ВМ, и 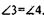т.е. AМ||ВС(1)
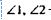- накрестлежащие углы при прямых АN и ВС и секущей NC
т.е. 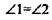АN||ВС (2)
Сравнивая (1) и (2) имеем:
АМ||АN, АN||ВС, значит АМ||АN, но так как прямые АМ и АN про-
ходят через одну точку А и параллельны одной и той же прямой ВС,
то, по аксиоме параллельных прямых можно утверждать, что АМ и
AN - совпадают, т.е.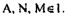
Или А. N. М лежат на прямой l ч.т.д.