Проведите §5 №50 ГДЗ Геометрия 7-9 класс Погорелов А.В.

Сначала построим окружность с центром O1 и радиусом - R2. Из центра O2 второй окружности проводим касательную к этой окружности (задача № 49). Касательная касается этой окружности в точке К.
 

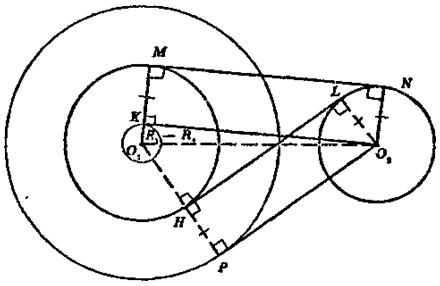
Рассмотрим всевозможные варианты:
1)         Если центр одной окружности лежит внутри другой и они не пересекаются, то касательную провести нельзя.
2)         Если центр одной окружности лежит внутри другой и они касаются в одной точке, то одна касательная.
3)         Если они пересекаются в двух точках, то две касательные.
4)         Если единственная точка пересечения лежит между их центрами, то три касательные.
5)         Если R₁ + R₂ < О₁О₂, то четыре касательных.
6)         Если R₁ = R₂ и O₂ совпадает с O₁, то бесконечное число касательных.