При параллельном переносе параллелограмм переходит в равный ему параллелограмм. ГДЗ. Геометрия. 10 класс. Погорелов. § 4 п.29 Задача 26

Докажите, что при параллельном переносе параллелограмм переходит в равный ему параллелограмм.

1 ответ

ответы

Макар Ильин

Пожаловаться

Лови доказательство.

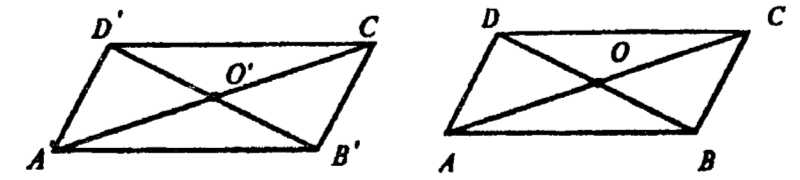
Пусть ABCD - данный параллелограмм, а А', В', С, D' - точки, в
которые переходят А, В, С, D. Т. к. при параллельном переносе плоскость переходит в параллельную ей плоскость (или в себя), то плоскость A'B'C'D' параллельна плоскости ABCD.
Т.к. при параллельном переносе точки смещаются по параллель-
ным (или совпадающим) прямым на одно и то же расстояние, то АА’ || ВВ' || СС || DD' и АА' = ВВ' = СС = DD'.
Так что в четырехугольнике AA'D'D противолежащие стороны
параллельны и ровны, а, значит, AA'D'D — параллелограмм. Тогда
Α'D' = AD и A'D’ || AD.
Аналогично А'В' = АВ и А'В' || AB; CD' = CD и CD' || CD;
B'C = ВС и В'С || ВС.
Т.к. две прямые, параллельные третьей, параллельны, то получаем, что A'D' || В’С, А'В' || CD'.
А, значит, A'B'C'D' — параллелограмм, равный параллелограмму
ABCD (т.к. соответствующие стороны равны). Что и требовалось
доказать.