Постройте треугольник §5 №47 ГДЗ Геометрия 7-9 класс Погорелов А.В.

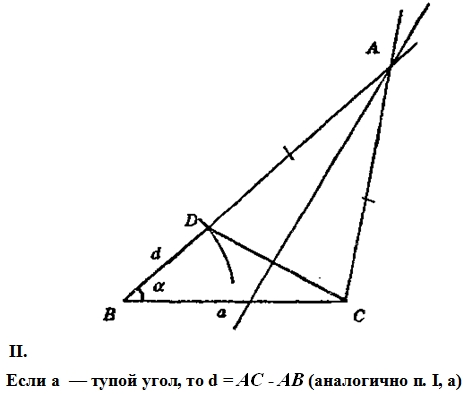
1. Допустим такой треугольник уже построен. Рассмотрим два случая:
 
Если АВ > АС, d = АС, то отложим на стороне АВ отрезок ВD - тогда АD =АВ -d= АС, т.е. точка А лежит на серединном
перпендикуляре к СD.
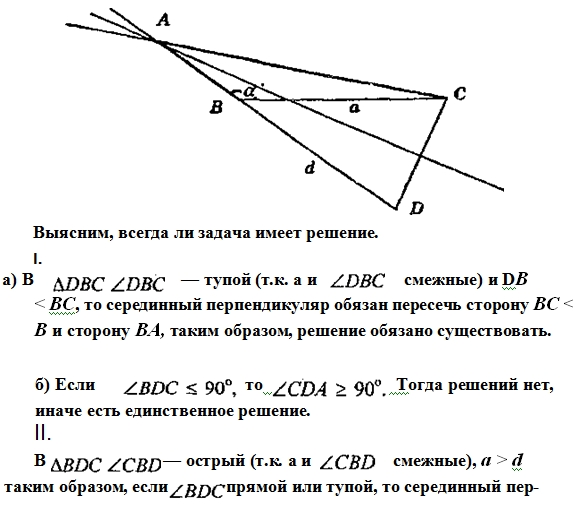
Если АС > АВ, то отложим на продолжении стороны АВ отрезок ВD = d.
d= АС - АВ, АD = АВ + ВD = АВ + d, т.е. АD = АС, поэтому точка А будет лежать на серединном перпендикуляре к СО.
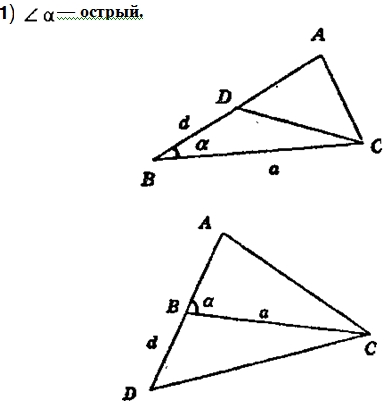
2) 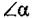 — тупой.
 
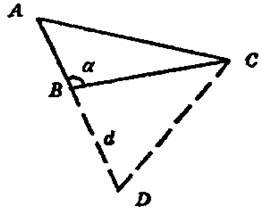
АС > АВ, тогда на продолжении сторона АВ отложим ВD = d,
тогда АD = АС и тогда точка А лежит на серединном
перпендикуляре к СD.
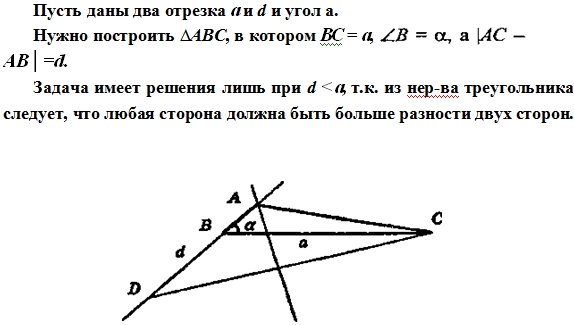
а)    Если а — острый угол, d =АС - АВ.
Построим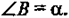
Отложим на одной стороне угла ВС = а, а на дополнительной
полупрямой к другой стороне ВО = d.
 
Отложим на одной стороне угла ВС = а, а на дополнительной
полупрямой к другой стороне ВО = d.