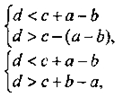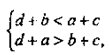Постройте трапецию §6 №71 ГДЗ Геометрия 7-9 класс Погорелов А.В.
Пусть даны отрезки a, b, с, d, такие, что в трапеции ABCD с ос-
нованиями AD и ВС AD = а; ВС = b;
АВ = с; DC = d (AD > ВС).
Пусть есть трапеция ABCD, удовлетворяющая таким условиям.
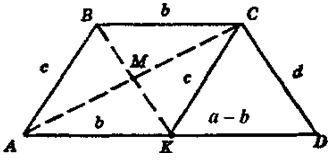
Проведем в трапеции ABCD прямую СК‖AВ, пересекающую AD в точке К. Получим параллелограмм АВСК, в котором СК = АВ = с; АК = ВС = b.
Далее рассмотрим AKCD:
КС = с; CD = d; KD = a-b.
Данный треугольник можно построить по трем известным сторонам. Тогда
Построим трапецию ABCD по плану:
1. На произвольной прямой от точки А отложим отрезок AD = а, на этом отрезке от точки А отложим отрезок АК = b.
2. Построим ΔKCD со сторонами KD = а - b;
КС = с; CD = d.
3. Построим параллелограмм АКСВ, для этого проведем через точки А и С прямые параллельные прямым СК и АК и пересекающиеся в точке В.
Докажем, что получившийся четырехугольник ABCD — искомая трапеция.
AD = а (по построению). ВС‖ЛК, BC‖AD, так как AВСК — параллелограмм по построению. ВС = b (по построению).
Если ВС ‖ AD, ВС = b; AD = а, то ABCD — трапеция с основаниями AD = а, ВС = b, удовлетворяющими условию задачи.
CD = d; СК = с (по построению).
АВ = СК = с, так как ABСK — параллелограмм. Боковые стороны CD и АВ удовлетворяют условию задачи.
Итак, ABCD — искомая трапеция.
Заметим, что задача имеет решения только если можно построить AKCD со сторонами d; с; а - b. Это возможно тогда и только тогда, когда одна сторона меньше суммы двух других, но больше разности двух других, то есть, при условиях:
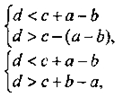
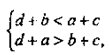
Так как в данной полуплоскости относительно KD можно построить только один ΔKCD с заданными сторонами, то решение, то есть искомая трапеция, будет единственным.
