Постройте сечение № 1188 ГДЗ Геометрия 9 класс Атанасян Л.С.
При построении сечений параллелепипеда нужно руководствоваться следующим правилом (оно будет обосновано в курсе стерео-метрии в 10 классе): отрезки, по которым секущая плоскость пересекает две противоположные грани параллелепипеда, параллельны.
1) Рассмотрим сначала случай расположения точек А, В и С, изображённый на рисунке 355, а. Проведём отрезки АВ и ВС.
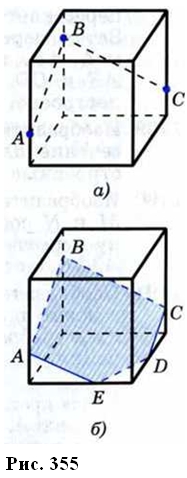
Далее, руководствуясь указанным правилом, через точку А проведём в плоскости «передней» грани прямую, параллельную ВС, а через точку С в плоскости боковой грани проведём прямую, параллельную АВ. Пересечения этих прямых с рёбрами нижней грани дают точки Е и D (рис. 355, б). Остаётся провести отрезок DE, и искомое сечение — пятиугольник ABCDE — построено.
2) Обратимся теперь к случаю, представленному на рисунке 356,а. Этот случай
более трудный, чем предыдущий. Можно провести отрезки АВ и ВС (см. рис. 356, а), но что делать дальше? Поступим так. Сначала построим прямую, по которой секущая плоскость пересекается с плоскостью нижнего основания параллелепипеда.
С этой целью продолжим отрезок АВ и нижнее ребро, лежащее в той же грани, что и отрезок АВ, до пересечения в точке М (рис. 356, б). Далее, через точку Мпроведём в плоскости нижнего основания
прямую, параллельную ВС. Это и есть та прямая, по которой секущая плоскость
пересекается с плоскостью нижнего основания. Эта прямая пересекается с рёбрами нижнего основания в точках Е и F. Затем через точку Е проведём прямую, параллельную прямой АВ, и получим точку D. Наконец, проведём отрезки AF и CD, и искомое сечение — шестиугольник ABCDEF —построено.
