Постройте ромб §6 №38 ГДЗ Геометрия 7-9 класс Погорелов А.В.
1) Строим данный угол и проводим биссектрису. От вершины биссектрисы откладываем диагональ АВ и делим ее пополам, точкой О. Проводим перпендикуляр через точку О к диагонали АВ, который пересекает стороны угла в точках С и D, которые являются вершинами искомого ромба.
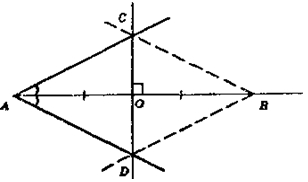
2) Пусть дан угол а и диагональ d. Необходимо построить ромб, в котором один из углов равен а, а противолежащая диагональ равна d.
Предположим, что существует ромб ABCD, в котором диагональ BD = d, и ∠BAD=a.
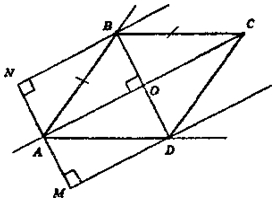
Диагональ АС — биссектриса ∠BAD и АС ⊥ BD. Проведем че-
рез точку А прямую ММ ⊥ AС и отложим отрезки
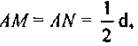
по разные стороны от точки А, следовательно, MNBD — прямо-
угольник.
Построим ∠BAD = α. Проведем биссектрису АС угла BAD. Че-
рез точку А проведем прямую MN ⊥ а и от точки А отложим
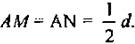
Проведем через М и N прямые, параллельные АС,
точки пересечения этих прямых со сторонами угла BAD обозна-
чим соответственно В и D. Раствором циркуля, равным АВ, прове-
дем дугу с центром В, при этом, точку пересечения дуги с прямой
а обозначим С. Получим четырехугольник ABCD.
Докажем, что ABCD — ромб в котором ∠BAD = α и BD = d.
∠BAD = α — по построению.
Так как MNBD — прямоугольник по построению, то отрезок
АО — серединный перпендикуляр к BD и ABAD — равнобедрен-
ный (AB=AD); ОС — серединный перпендикуляр в ABCD, значит,
ΔBCD — равнобедренный (ВС = CD). Так как АВ = ВС по по-
строению, то AB=BC=CD=AD и ABCD — ромб с ∠BAD = α.
По построению BD = MN = d, значит, ABCD — искомый ромб.
