Постройте §6 №72 ГДЗ Геометрия 7-9 класс Погорелов А.В.
Даны отрезки a, b, d1 и d2. Необходима построить трапецию ABCD (с основаниями AD и ВС, AD > ВС), такую, что AD = а; ВС = b; АС = d; BD = d2.
Допустим, что ABCD — искомая трапеция.
Тогда на продолжении AD отложим отрезок DE = b, Следовательно, DBCE — параллелограмм, так как две его стороны ВС и DE параллельны и равны. Поэтому стороны BD и СЕ параллельны и равны: BD=CE=d2.
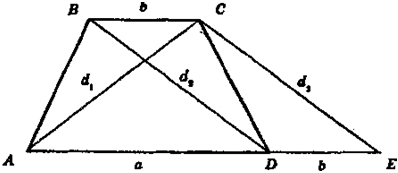
Рассмотрим ΔАСЕ. АС = d1; СЕ = d2; АЕ = а + b.
План построения трапеции:
1) На произвольной прямой отложим отрезок AD = а. На продолжении AD отложим отрезок DE = b.
2) Построим ΔАСЕ по известным сторонам АЕ = а + b; АС = d1; СЕ = d2.
3) Через точку С проведем прямую, параллельную АЕ, и на этой прямой от точки С в ту же полуплоскость относительно СЕ, где и точка А, отложим отрезок СВ = b.
4) Получим четырехугольник ABCD. Докажем, что ABCD искомая трапеция.
BC‖AD (по построению). Так как AD ≠ ВС (по условию), то ABCD не является параллелограммом, а значит, является трапецией с основаниями AD = а, ВС = b (по построению).
По построению диагональ АС = d1; СЕ = d2. Так как BCED — параллелограмм (его противоположные стороны ВС и DE по построению параллельны и равны), то BD = СЕ = d2.
Значит, диагонали АС и ВD равны соответственно d1 и d2, и следовательно, ABCD — искомая трапеция. Заметим, что задача
имеет решения не всегда, а только в случае если можно построить ΔАСЕ со сторонами в + b, d1 и d2. Это возможно тогда и только тогда, когда одна сторона больше разности двух, других и меньше суммы двух других, то есть, когда |d2 - d1 |< а + b < d2 + d1. В этом случае ΔАСЕ определяется однозначно и задача имеет единственное решение. В других случаях ΔАСЕ построить нельзя и задача решений не имеет.
